图灵机加法器优化
前置信息
警告⚠
本文提供了完整的源代码,此源代码不可照搬用于作业中。计算机科学导论课有代码查重环节,其中可以检测出包括但不限于单纯的变量替换和代码块打乱等避查手段。抄袭严重违反学术诚信和学术道德,而且如果被检测出作弊将会直接取消该项成绩。
通过查重的最好办法就是自己重新动手写一个
图灵机形式化定义
- 图灵机是一个七元组M={Q, Σ, Γ, δ, q0, qAccept, qReject },其中 Q, Σ, Γ 都是有限非空集合。
- 状态集合 Q 。
- 输入字母表 Σ (所有的可能输入元素构成的集合e.g.{0,1})。
- 带字母表 Γ:存在特殊字符B∈Γ,表示空白符号,要求B∉Σ 且 Σ⊂Γ。(可以比B多,比如@$#等图灵机写的符号)
- 转移函数δ :(Q-{qAccept, qReject })×Γ → Q×Γ×{→,←}。
- 起始状态:q0 ∈ Q。
- 接受状态:qAccept ∈ Q。
- 拒绝状态:qReject ∈ Q。
代码规范
图灵机的转移规则由代码形式给出,其中一个转移规则占一行。一个转移规则的代码基本结构由四个逗号分隔开的五个符号表示。形如q0, B, 0, R, q1的代码表示规则“在q0状态下某位置读写头读取到B,则将该位置符号改写为0,随后向右移动一格并进入q1状态”。
注意:本题目要求的图灵机读写头在每一步必须既读又写,所以如果遇到不改写的规则可以通过读写同一个字符来实现。
题目信息
题目一
- 题面:请设计一个可以完成4位二进制数加法的图灵机。
- 格式要求:
- 输入:(4位0或者1)+(4位0或者1)=
- 停机时纸带:…###(5位0或者1)B###...
- 输入的“4位0或者1”表示要做加法的二进制数;
- 停机时纸带上的“5位0或者1” 作为答案(结果只有4位时注意加前导0),起始位置应为输入中“=” 位置右侧一格,并以 B 作为结尾。# 为 Γ 中任意字母。
- 样例:
- 输入: 1101+0011=
- 停机时纸带:…1101+0011=10000B…
- 输入: 0001+0011=
- 停机时纸带: …001101101 00100B000…
注: 输出中蓝色的“0”和输入中“=”的位置相同,即要求对齐
题目二
-
题面:设计一个可以完成任意位二进制数加法的图灵机。
-
格式要求:
- 输入:(若干0或者1)+(若干0或者1)=
- 停机时纸带:…###(若干0或者1)B###...
- 输入的“若干0或者1”中不含前导0;每一个操作数的长度大于等于1。
- 停机时纸带上的“若干0或者1”作为答案,不应含有前导0。答案的起始位置应为输入中 “=” 位置右侧一格,并以 B 作为结尾。# 为 Γ 中任意字母。
-
样例:
- 输入: 11+1001=
- 停机时纸带:…wRQTqLaA1100BssR…
注: 输出中的“A”和输入中“=”的位置相同
问题二题解
目标总述
这几个问题做出来并不难,但是我们毕竟是有追求的人——本篇集中对于这两个问题的优化而非求解进行讨论。就像一般程序优化的方向一样,图灵机编程也有两个优化指标——时间复杂度和空间复杂度。但是这两个复杂度指标和一般的程序复杂度有稍许区别。因为在满血图灵机中,存储设备(纸带)是无限的,而转移表是有限的,因此优化空间复杂度就是尽量减少转移表规则数(也就是图灵机代码行数)。而时间复杂度则是对应的完成任务所需步数。
这两个优化方向在进行到一定程度以后通常变得相互矛盾——为了最求一个复杂度的极致优化,我们必须要牺牲另外一个复杂度。20级同学在求解这两道问题时在空间复杂度上有了很多的进展,作为21级同学,我这里选择另一条道路:追求时间复杂度的极致优化。(P.S.在最后的小组报告时,我作为演讲者上台,提问环节老师就问了我这样一个问题:“写图灵机程序时,优化时间复杂度和空间复杂度哪一个更重要”。最后老师给出的答案是优化时间复杂度更重要,因为我们写的程序对于使用者而言是一个黑箱,他们感知最大的是程序的运行速度,而程序的行数他们并不是太在意)
这两个问题中,我主要针对问题二这种普适情况进行优化,并没有对问题一进行特别的专有优化。原因也很简单,问题一的输入是有限个(而且个数相当少),步数最少的算法一定是打表穷举。当然,我们针对问题一我的主要优化方向是追求用尽可能少的改动使得问题三的代码可以用于问题二的求解上。
V1.0代码
V1.0代码实现了最基本的问题求解思路
- 核心思想:设输入为A+B=,先将A加到B上得到C,再将C搬运到等号右侧
- 按照模块化的思想:将整个搬运过程分为计算部分和搬运部分
- 整个代码模拟人进行二进制加法的过程(朴素思想)
// x=0 ; y=1
// # to right ; $ to left
// assume the input is A + B =
q0,0,0,R,rightend
q0,1,1,R,rightend
q0,+,+,R,rightend
rightend,0,0,R,rightend
rightend,1,1,R,rightend
rightend,+,+,R,rightend
rightend,x,x,R,rightend
rightend,y,y,R,rightend
rightend,#,#,R,rightend
rightend,=,=,L,locate
locate,#,#,L,locate
locate,0,#,L,B0_sectionB
locate,1,#,L,B1_sectionB
locate,+,+,L,formatanswer
B0_sectionB,0,0,L,B0_sectionB
B0_sectionB,1,1,L,B0_sectionB
B0_sectionB,+,+,L,B0_sectionA
B1_sectionB,0,0,L,B1_sectionB
B1_sectionB,1,1,L,B1_sectionB
B1_sectionB,+,+,L,B1_sectionA
B0_sectionA,x,x,L,B0_sectionA
B0_sectionA,y,y,L,B0_sectionA
B0_sectionA,0,x,R,rightend
B0_sectionA,B,x,R,rightend
B0_sectionA,1,y,R,rightend
B1_sectionA,x,x,L,B1_sectionA
B1_sectionA,y,y,L,B1_sectionA
B1_sectionA,0,y,R,rightend
B1_sectionA,B,y,R,rightend
B1_sectionA,1,x,L,carry1
carry1,0,1,R,rightend
carry1,B,1,R,rightend
carry1,1,0,L,carry1
formatanswer,x,x,L,formatanswer
formatanswer,y,y,L,formatanswer
formatanswer,0,x,L,formatanswer
formatanswer,1,y,L,formatanswer
formatanswer,B,B,R,readanswer
readanswer,x,$,R,setx
readanswer,y,$,R,sety
readanswer,#,#,R,readanswer
readanswer,+,+,R,qa
setx,x,x,R,setx
setx,y,y,R,setx
setx,1,1,R,setx
setx,0,0,R,setx
setx,+,+,R,setx
setx,=,=,R,setx
setx,#,#,R,setx
setx,B,0,L,resetpointer
sety,x,x,R,sety
sety,y,y,R,sety
sety,0,0,R,sety
sety,1,1,R,sety
sety,+,+,R,sety
sety,=,=,R,sety
sety,#,#,R,sety
sety,B,1,L,resetpointer
resetpointer,x,x,L,resetpointer
resetpointer,y,y,L,resetpointer
resetpointer,0,0,L,resetpointer
resetpointer,1,1,L,resetpointer
resetpointer,+,+,L,resetpointer
resetpointer,=,=,L,resetpointer
resetpointer,#,#,L,resetpointer
resetpointer,$,$,R,readanswer
V2.0代码
Features:
- 减少寻址路程,第一版本的寻址停止标志为等号,每一次指针都要遍历所有的元素,改进后寻址停止标志为#号,随着程序的不断运行寻址步数将减少
- 单bit采用半加器结构,增加溢出位,将1+1的情况记为溢出符号z,然后进位方式为先溢出后统一进位
// x=0 ; y=1 ;z = 2
// # to right ; $ to left
// assume the input is A + B =
q0,0,0,R,rightend
q0,1,1,R,rightend
q0,+,+,R,rightend
rightend,0,0,R,rightend
rightend,1,1,R,rightend
rightend,+,+,R,rightend
rightend,x,x,R,rightend
rightend,y,y,R,rightend
rightend,z,z,R,rightend
rightend,B,B,R,rightend
rightend,#,#,L,locate
rightend,=,#,L,locate
locate,#,#,L,locate
locate,0,#,L,B0_sectionB
locate,1,#,L,B1_sectionB
locate,+,+,L,formatanswer
B0_sectionB,0,0,L,B0_sectionB
B0_sectionB,1,1,L,B0_sectionB
B0_sectionB,+,+,L,B0_sectionA
B1_sectionB,0,0,L,B1_sectionB
B1_sectionB,1,1,L,B1_sectionB
B1_sectionB,+,+,L,B1_sectionA
B0_sectionA,x,x,L,B0_sectionA
B0_sectionA,y,y,L,B0_sectionA
B0_sectionA,z,z,L,B0_sectionA
B0_sectionA,0,x,R,rightend
B0_sectionA,B,x,R,rightend
B0_sectionA,1,y,R,rightend
B1_sectionA,x,x,L,B1_sectionA
B1_sectionA,y,y,L,B1_sectionA
B1_sectionA,z,z,L,B1_sectionA
B1_sectionA,0,y,R,rightend
B1_sectionA,B,y,R,rightend
B1_sectionA,1,z,R,rightend
formatanswer,x,x,L,formatanswer
formatanswer,y,y,L,formatanswer
formatanswer,z,x,L,carry1
formatanswer,0,x,L,formatanswer
formatanswer,1,y,L,formatanswer
formatanswer,B,B,R,readanswer
carry1,x,y,L,formatanswer
carry1,y,x,L,carry1
carry1,z,y,L,carry1
carry1,0,y,L,formatanswer
carry1,1,x,L,carry1
carry1,B,y,L,formatanswer
readanswer,x,$,R,setx
readanswer,y,$,R,sety
readanswer,#,#,R,readanswer
readanswer,+,+,R,qa
setx,x,x,R,setx
setx,y,y,R,setx
setx,1,1,R,setx
setx,0,0,R,setx
setx,+,+,R,setx
setx,=,=,R,setx
setx,#,#,R,setx
setx,B,0,L,resetpointer
sety,x,x,R,sety
sety,y,y,R,sety
sety,0,0,R,sety
sety,1,1,R,sety
sety,+,+,R,sety
sety,=,=,R,sety
sety,#,#,R,sety
sety,B,1,L,resetpointer
resetpointer,x,x,L,resetpointer
resetpointer,y,y,L,resetpointer
resetpointer,0,0,L,resetpointer
resetpointer,1,1,L,resetpointer
resetpointer,+,+,L,resetpointer
resetpointer,=,=,L,resetpointer
resetpointer,#,#,L,resetpointer
resetpointer,$,$,R,readanswer
V3.0代码
Features:
- 创新点:将一次对一个bit进行加法改进为一次对两个bit进行加法,这样加法运算的寻址步数可以接近减半。
- 创新点:将一次搬运一个bit改进为一次搬运两个bit,这样来回搬运的趟数可以接近减半。
- 2bit的操作方法是进行暴力枚举
q0,0,0,R,q0
q0,1,1,R,q0
q0,+,+,L,scanA
locateequal,+,+,R,locateequal
locateequal,0,0,R,locateequal
locateequal,1,1,R,locateequal
locateequal,x,x,R,locateequal
locateequal,y,y,R,locateequal
locateequal,z,z,R,locateequal
locateequal,=,=,L,formatanswer
scanA,0,+,L,Ax0
scanA,1,+,L,Ax1
scanA,+,+,L,scanA
scanA,B,B,R,locateequal
Ax0,0,+,R,A00
Ax0,1,+,R,A10
Ax0,B,B,R,AB0
Ax1,0,+,R,A01
Ax1,1,+,R,A11
Ax1,B,B,R,AB1
A00,0,0,R,A00
A00,1,1,R,A00
A00,+,+,R,A00
A00,=,=,L,add002
A00,x,x,L,add002
A00,y,y,L,add002
A00,z,z,L,add002
A10,0,0,R,A10
A10,1,1,R,A10
A10,+,+,R,A10
A10,=,=,L,add102
A10,x,x,L,add102
A10,y,y,L,add102
A10,z,z,L,add102
A01,0,0,R,A01
A01,1,1,R,A01
A01,+,+,R,A01
A01,=,=,L,add012
A01,z,z,L,add012
A11,0,0,R,A11
A11,1,1,R,A11
A11,+,+,R,A11
A11,=,=,L,add112
A11,x,x,L,add112
A11,y,y,L,add112
A11,z,z,L,add112
AB0,0,0,R,AB0
AB0,1,1,R,AB0
AB0,+,+,R,AB0
AB0,=,=,L,addB02
AB0,x,x,L,addB02
AB0,y,y,L,addB02
AB0,z,z,L,addB02
AB1,0,0,R,AB1
AB1,1,1,R,AB1
AB1,+,+,R,AB1
AB1,=,=,L,addB12
AB1,x,x,L,addB12
AB1,y,y,L,addB12
AB1,z,z,L,addB12
add002,0,x,L,add001
add002,1,y,L,add001
add002,+,x,L,add001
add102,0,x,L,add101
add102,1,y,L,add101
add102,+,x,L,add101
add012,0,y,L,add011
add012,1,z,L,add011
add012,+,y,L,add011
add112,0,y,L,add111
add112,1,z,L,add111
add112,+,y,L,add111
addB02,0,x,L,locateequal
addB02,1,y,L,locateequal
addB02,+,x,L,locateequal
addB12,0,y,L,locateequal
addB12,1,z,L,locateequal
addB12,+,y,L,locateequal
add001,0,x,L,trans
add001,1,y,L,trans
add001,+,x,L,trans
add011,0,x,L,trans
add011,1,y,L,trans
add011,+,x,L,trans
add101,0,y,L,trans
add101,1,z,L,trans
add101,+,y,L,trans
add111,0,y,L,trans
add111,1,z,L,trans
add111,+,y,L,trans
trans,0,0,L,trans
trans,1,1,L,trans
trans,+,+,L,scanA
formatanswer,x,x,L,formatanswer
formatanswer,y,y,L,formatanswer
formatanswer,z,x,L,carry1
formatanswer,0,x,L,formatanswer
formatanswer,1,y,L,formatanswer
formatanswer,+,+,R,readanswer
carry1,x,y,L,formatanswer
carry1,y,x,L,carry1
carry1,z,y,L,carry1
carry1,0,y,L,formatanswer
carry1,1,x,L,carry1
carry1,+,y,L,formatanswer
readanswer,x,+,R,read0x
readanswer,y,+,R,read1x
read0x,x,+,R,set001
read0x,y,+,R,set011
read0x,=,=,R,set0B1
read1x,x,+,R,set101
read1x,y,+,R,set111
read1x,=,=,R,set1B1
readanswer,=,=,R,qa
set001,x,x,R,set001
set001,y,y,R,set001
set001,=,=,R,set001
set001,1,1,R,set001
set001,0,0,R,set001
set001,B,0,R,set002
set011,x,x,R,set011
set011,y,y,R,set011
set011,=,=,R,set011
set011,1,1,R,set011
set011,0,0,R,set011
set011,B,0,R,set012
set101,x,x,R,set101
set101,y,y,R,set101
set101,=,=,R,set101
set101,1,1,R,set101
set101,0,0,R,set101
set101,B,1,R,set102
set111,x,x,R,set111
set111,y,y,R,set111
set111,=,=,R,set111
set111,1,1,R,set111
set111,0,0,R,set111
set111,B,1,R,set112
set0B1,x,x,R,set0B1
set0B1,y,y,R,set0B1
set0B1,=,=,R,set0B1
set0B1,1,1,R,set0B1
set0B1,0,0,R,set0B1
set0B1,B,0,L,qa
set1B1,x,x,R,set1B1
set1B1,y,y,R,set1B1
set1B1,=,=,R,set1B1
set1B1,1,1,R,set1B1
set1B1,0,0,R,set1B1
set1B1,B,1,L,qa
set002,B,0,L,resetpointer
set102,B,0,L,resetpointer
set012,B,1,L,resetpointer
set112,B,1,L,resetpointer
resetpointer,x,x,L,resetpointer
resetpointer,y,y,L,resetpointer
resetpointer,0,0,L,resetpointer
resetpointer,1,1,L,resetpointer
resetpointer,=,=,L,resetpointer
resetpointer,+,+,R,readanswer
V4.0代码
Features:
- 将半加器结构改进为全加器结构。改进后可以节省最后统一进位的一趟位移。
- 创新点: 针对策略分支更加复杂的情况将第二位数字加法的可能进行合并,相对于暴力穷举减少重复的策略。(e.g.10和00搬运第二位都是0,这样就可以合并策略减少重复的分支)
- 创新点:合并后的策略又针对特殊情况进行了优化(比如最后一次搬运只需要搬运一个字符的情况)
// x=0 ; y=1
// use + to clean the written letter
// assume the input is A + B =
q0,0,0,R,q0
q0,1,1,R,q0
q0,+,+,L,scanA
scanA,0,+,L,Ax0
scanA,1,+,L,Ax1
scanA,+,+,L,scanA
scanA,B,B,R,readanswer
Ax0,0,+,R,A00
Ax0,1,+,R,A10
Ax0,B,B,R,AB0
Ax1,0,+,R,A01
Ax1,1,+,R,A11
Ax1,B,B,R,AB1
A00,0,0,R,A00
A00,1,1,R,A00
A00,+,+,R,A00
A00,=,=,L,add00
A00,x,x,L,add00
A00,y,y,L,add00
A10,0,0,R,A10
A10,1,1,R,A10
A10,+,+,R,A10
A10,=,=,L,add10
A10,x,x,L,add10
A10,y,y,L,add10
A01,0,0,R,A01
A01,1,1,R,A01
A01,+,+,R,A01
A01,=,=,L,add01
A01,x,x,L,add01
A01,y,y,L,add01
A11,0,0,R,A11
A11,1,1,R,A11
A11,+,+,R,A11
A11,=,=,L,add11
A11,x,x,L,add11
A11,y,y,L,add11
AB0,0,0,R,AB0
AB0,1,1,R,AB0
AB0,+,+,R,AB0
AB0,=,=,L,addB0
AB0,x,x,L,addB0
AB0,y,y,L,addB0
AB1,0,0,R,AB1
AB1,1,1,R,AB1
AB1,+,+,R,AB1
AB1,=,=,L,addB1
AB1,x,x,L,addB1
AB1,y,y,L,addB1
add00,0,x,L,add0
add00,1,y,L,add0
add00,+,x,L,add0
add10,0,x,L,add1
add10,1,y,L,add1
add10,+,x,L,add1
add01,0,y,L,add0
add01,1,x,L,add1
add01,+,y,L,add0
add11,0,y,L,add1
add11,1,x,L,add2
add11,+,y,L,add1
addB0,0,x,L,locateplus
addB0,1,y,L,locateplus
addB0,+,x,L,locateplus
addB1,0,y,L,locateplus
addB1,1,x,L,Bcarry1
addB1,+,y,L,locateplus
add0,0,x,L,return
add0,1,y,L,return
add0,+,x,L,return
add1,0,y,L,return
add1,1,x,L,carry1
add1,+,y,L,return
add2,0,x,L,carry1
add2,1,y,L,carry1
add2,+,x,L,carry1
return,0,0,L,return
return,1,1,L,return
return,+,+,L,scanA
carry1,0,1,L,return
carry1,1,0,L,carry1
carry1,+,1,L,return
Bcarry1,0,1,L,locateplus
Bcarry1,1,0,L,Bcarry1
Bcarry1,+,1,L,locateplus
locateplus,1,1,L,locateplus
locateplus,0,0,L,locateplus
locateplus,+,+,R,readanswer
readanswer,x,+,R,read0x
readanswer,0,+,R,read0x
readanswer,y,+,R,read1x
readanswer,1,+,R,read1x
readanswer,+,+,R,readanswer
read0x,x,+,R,set00
read0x,0,+,R,set00
read0x,y,+,R,set01
read0x,1,+,R,set01
read0x,=,=,R,set0B
read1x,x,+,R,set10
read1x,0,+,R,set10
read1x,y,+,R,set11
read1x,1,+,R,set11
read1x,=,=,R,set1B
readanswer,=,=,R,qa
set00,x,x,R,set00
set00,y,y,R,set00
set00,=,=,R,set00
set00,1,1,R,set00
set00,0,0,R,set00
set00,B,0,R,set0
set01,x,x,R,set01
set01,y,y,R,set01
set01,=,=,R,set01
set01,1,1,R,set01
set01,0,0,R,set01
set01,B,0,R,set1
set10,x,x,R,set10
set10,y,y,R,set10
set10,=,=,R,set10
set10,1,1,R,set10
set10,0,0,R,set10
set10,B,1,R,set0
set11,x,x,R,set11
set11,y,y,R,set11
set11,=,=,R,set11
set11,1,1,R,set11
set11,0,0,R,set11
set11,B,1,R,set1
set0B,x,x,R,set0B
set0B,y,y,R,set0B
set0B,=,=,R,set0B
set0B,1,1,R,set0B
set0B,0,0,R,set0B
set0B,B,0,L,qa
set1B,x,x,R,set1B
set1B,y,y,R,set1B
set1B,=,=,R,set1B
set1B,1,1,R,set1B
set1B,0,0,R,set1B
set1B,B,1,L,qa
set0,B,0,L,resetpointer
set1,B,1,L,resetpointer
resetpointer,x,x,L,resetpointer
resetpointer,y,y,L,resetpointer
resetpointer,0,0,L,resetpointer
resetpointer,1,1,L,resetpointer
resetpointer,=,=,L,resetpointer
resetpointer,+,+,R,readanswer
转移图:(右键新标签页中打开查看高清大图)
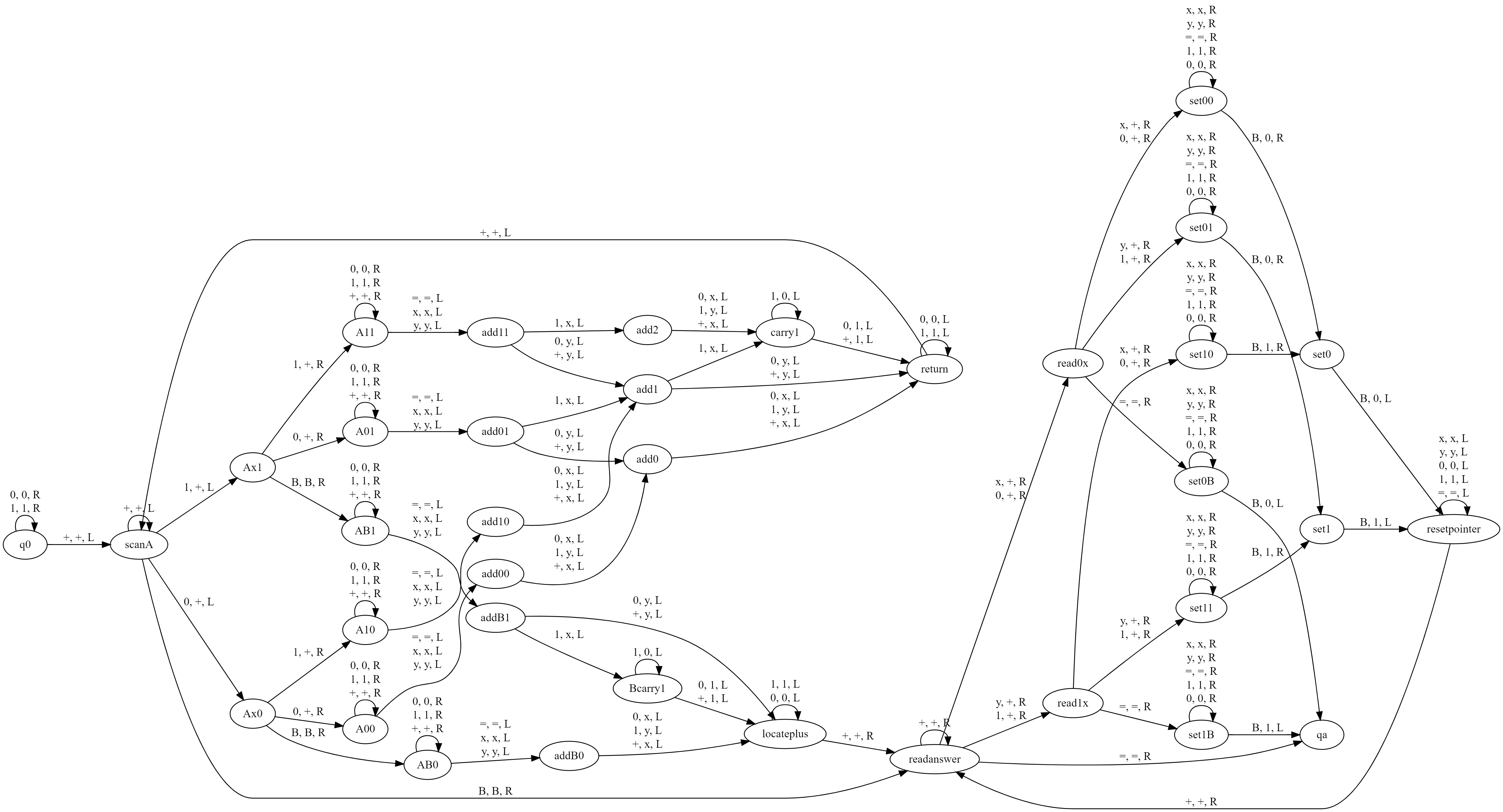
问题一题解
核心思想是想办法如何照搬问题二的代码,这样做一道题的功夫实际上解了两道题。对比发现适配问题一需要解决前导0问题。
创新点:仅仅改动问题二代码中的一个字符实现补0要求

输入A+B=,在q0状态向右移动读写头去定位加式中的+时,将+改为0后向再左进入读取A的状态实现在B的左侧手动补0。随后的过程与第三问完全一致。
可以证明这种方案可以完成第二问要求的补0操作
- 如果本来计算结果是4位,那么此操作相当于添加了补0
- 如果本来计算结果是5位,那么此操作不影响进位,可以正确输出5位答案
总结
个人认为我目前的进度已经将这个方向的优化做到极致了,上升空间已经变和非常之小。剩下的优化无非就是一次搬运更多的位数,但是这种局部穷举的思想并不符合图灵机的指导思想,而且迈出“一次搬运两位”的跨越式改进以后剩下的就只剩简单重复的工作了。如果有兴趣,可以写出一次搬运3位甚至更多位的图灵机,但是这样意义就显得微乎其微了(更别说这样做的代价是代码行数以近指数倍数进行增长)。
附老师测试的10个数据点成绩:
| 计算项目 | 步数 |
|---|---|
| 1+1= | 22 |
| 1+0= | 13 |
| 11+10= | 33 |
| 1111+1011= | 77 |
| 101010+11010101= | 168 |
| 1010000101+101010= | 240 |
| 101001000001+1011010= | 323 |
| 111111111111+1111111111= | 387 |
| 101011101011+101011101= | 349 |
| 10011111+10000010010001= | 388 |
| Total | 2000 |